Your everyday world from a physicist's perspective
Throwing things: stability of rotation
Anyone with experience in throwing things, may have noticed the following remarkable feature: sometimes the object keeps on rotating more or less stable about the same axis, while other times the motion is a complete mess.

In the above figure I threw one of my textbooks on classical mechanics up in the air three times, each time giving it an initial spin about a different axis of symmetry. I had to put on some tape to make sure the book did not open up in mid air. If you happen to have some solid, book shaped (rectangular) object at hand, then you can try it for yourself.
The first and second picture show a stable rotation, while in the third throw the book tumbled like a drunken acrobat. The question is: why?
Even though the question is quite clear, it is not possible to give the answer at first sight (at least not for me). We shall need some sophisticated line of reasoning, based on the 'laws of tumbling bodies' discovered by Euler to tackle this one.
A physicist's explanation
The general law of tumbling objects
We start by stating Euler's law for tumbling solid objects. In mathematical notation it reads
(1)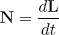 .
.
In words: the rate of change of the total angular momentum L of the body is equal to the net external torque N applied to the body. Or in other words: if one applies a "twist" (by hand or with a motor) to an object, it will start rotating faster or slower or change its orientation (depending on the direction of the twist). If one does nothing to the object (and there is also no friction), it will just keep on tumbling in the same way it did before (this is called the law of conservation of angular momentum and it is very general, although no-one really understands why things behave in this way).
Before we can make any precise deductions from the (postulated) law of tumbling objects, I'll have to tell you what "we physicist's" mean by "the angular momentum L of the body". For symmetric objects (like books) L can be expressed as
(2)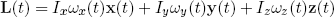 ,
,
where x, y, and z are orthogonal unit vectors along the axes of symmetry (which will be pointing in different directions all the time as the object tumbles about), the ω's are the instantaneous angular frequencies about these axes (in rad/sec) and the I's are constants (called 'moments of inertia') that depend on the distribution of mass about the specific axis of symmetry, I ~ mass*(distance from rotation axis)2.
Let's plug the expression for L into Newton's law for tumbling
(3)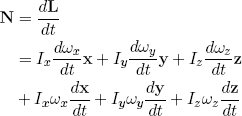 .
.
I used the product rule of differentiation to expand terms like d[ωx(t)x(t)]/dt. As one can easily check, the rate of change of symmetry axis x as the object rotates about, can be expressed as dx/dt = ω × x, where ω = (ωx, ωy, ωz) and × denotes the cross product of vector algebra. A similar expression holds for the rates of change of y and z, so we can write
(4)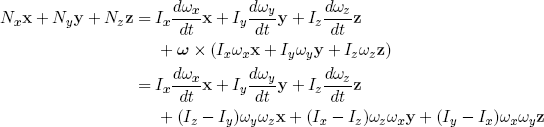 ,
,
where in the last expression I explicitly expanded the cross product. Since the axes are orthogonal, we can write this single vector equation as three separate (but coupled) equations for each of the components
(5)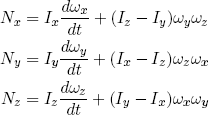 .
.
These equations are called the 'Euler equations of rotation'. I have cheated a bit by saying that one should take axes of symmetry, implying that this equation only holds for symmetric objects. But it turns out that for any rigid solid object (even for a potato!) one can find a set of orthogonal axes x, y and z so that this equation is true. These special axes are called the 'principal axes of inertia', and for symmetric objects they happen to coincide with the axes of symmetry.
With this last set of equations we have all the basic ingredients to analyze the tumbling book.
Stability of the tumbling book
In the following I will (as convention) always take the axis about which the book is given its initial spin to be the x-axis. The I's will then change depending on how we hold the book.
Now, when the book is up in the air, there is no net twist acting on it (neglecting the friction with the air of course, which is not important for heavy objects like books), so we have N = 0. It is easy to see that for N = 0, the Euler equations always have a solution of the form ωx = const, ωy = 0 and ωz = 0 (no matter what the values of the I's are). This means that if we start the rotation exactly about one of the axes of symmetry of the book, it will just keep on rotating about that axis with constant angular velocity.
But as you might guess, it is not easy (if not impossible) to start the rotation precisely about a given axis. So, to take a slight initial deviation into account we can try
(6)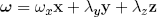 ,
,
where λy(t) and λz(t) are very small (but finite) rotational components about the y and z axes respectively. If we put this into the Euler equations and neglect small terms of order λ2 (thus implicitly assuming they will remain small) we get
(7)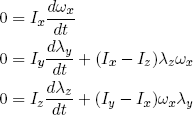 .
.
From the first equation we see that ωx = const. Using this, we can differentiate the second equation with respect to t and plug in the third equation to find a differential equation involving only λy and a constant which we will call Ω2:
(8)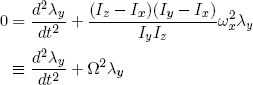 .
.
As one might know from calculus, this equation has a general solution of the form
(9)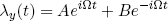 ,
,
where A and B are constants that depend on the specific initial conditions for λ. For example, if we take λ(0) = λ0 and dλ/dt(0) = 0, we find
(10)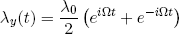 .
.
Now let's see what this equation will tell us for the different orientations of the book:
- The first of the orientations demonstrated at the beginning of this article corresponds to Iy > Iz > Ix. As one can see from equation 8 this implies that Ω is a positive real number, so that equation 10 represents a small, bounded wobbling of the form λ(t) = λ0cos(Ωt).
- The second orientation corresponds to Ix > Iy > Iz. So again Ω is real and will we have only a small additional wobbling superimposed on an overall stable rotation.
- In the third orientation we have Iz > Ix > Iy. This time Ω2 in equation 8 is negative, thus Ω must be a complex number! This means that λ(t) will be of the form exp(Ωt), which grows without bound (at some point invalidating the assumption that λ remains small). This mathematical behavior corresponds to the observed instability of rotation about this axis!
So by using the laws of tumbling and some sophisticated mathematical reasoning we can now more or less understand why rotating objects can behave very different when given an initial spin about different axes of symmetry. The mathematical method of doing stability analysis outlined above (assuming small deviations and then see how they behave in time, etc) is a very powerful tool that is used in many areas of physics and other sciences, for example in analyzing the onset of turbulence in fluid flows.
The special case of a frisbee
There is one special case of this theory of rotation that is very interesting and amusing: that of throwing a flat disk (for example a frisbee). For a thin disk one can show that the moments of inertia are related as Iy = Iz = Ix/2, so that according to equation 8 we have Ω = ωx, i.e. independent of actual values of I. Another way to see this is by imagining that one is spinning along with the frisbee. In this 'frame of reference' there will be an outward centrifugal force of magnitude m*r*ωx2 on each piece of mass m inside the frisbee. This force behaves similar to a gravitational force m*g with g = r*ωx2. Now, a pendulum of length r and mass m that swings in a gravitational field has a frequency (for small oscillations) Ω = √(g/r). Putting in our 'centrifugal gravity' we get Ω = ωx as before.
So a frisbee (or some other kind of spinning disk) always wobbles with a frequency approximately twice its spinning frequency! (Twice, because the axis with respect to which we measure λy is itself spinning with ωx radians per second.)
References
- Thornton and Marion (2004), Classical Dynamics of Particles and Systems 5th ed., Brooks/Cole, ISBN 0-534-40896-6
