Your everyday world from a physicist's perspective
Tapeline transitions
This time we will dig into the wonderful world of an indispensable measurement tool: the retractable tapeline.

The great thing about tapelines is that they can bridge considerable distances before snapping (2 m or so), while at the same time being easily portable. Now, how can a thin (0.1 mm) sheet of metal remain practically straight for such long extensions?
The short answer is curvature. The metal sheet that comes out of the holder has a slightly curved cross sectional area. Depending on the circumstances it will behave like a stiff rod or like a flexible sheet.
Let us look into this dual behavior in a bit more detail. We will begin our explorations by a closer inspection of the buckled state (see figure 2).

In the buckled state the tapeline consists of two undeformed, almost straight legs, connected by a flattened part which seems to describe a part of a circle with a diameter of approximately 2 cm. An interesting feature of the flat part is that its radius of curvature is independent of how far apart one holds the two legs. If you happen to have a tapeline at hand, try it.
And while you are at it, also convince yourself of the fact that once you let the tapeline become straight again, there are no visible traces of the buckling (no cracks or dents). In other words: all deformations happen within the elastic regime of the metal sheet.
The radius of the flat part
To find the equilibrium shape of the tapeline in the buckled state we can use the general and very powerful principle that the entropy* in the world tends to become a maximum (see the story about a rubber band for details).
The tapeline can freely exchange energy with its surroundings, so when the tapeline reaches its final shape we must have that the total entropy,
(1)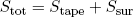 ,
,
is a maximum (at constant total volume and energy). This means that any slightly different shape of the tapeline will have a lower total entropy associated with it. In other words
(2)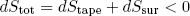 .
.
By our definition of temperature, a small change dEsur in the energy of the surroundings (at constant volume) implies a change
(3)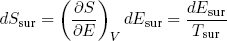 ,
,
in its entropy. From the conservation of energy we know
(4)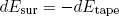 .
.
If we finally suppose that everything happens at one temperature T, then we find by combining equation (2), (3) and (4)
(5)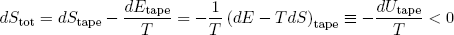 .
.
So in order to maximize the total entropy in the world at fixed temperature and volume, we must minimize (note the minus sign) a thing called the 'free energy' or 'potential energy' U of the tapeline. Where U is taken as
(6)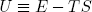 ,
,
so that
(7)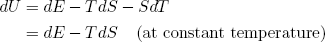 ,
,
as required by equation (5).
To get a feeling for the meaning of U, let us go back to the case of the rubber band for a moment. There we found
(8)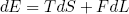 ,
,
where F is the force by which the rubber bands pulls back upon extension. If we plug this into equation (7), we find
(9)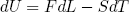 ,
,
so that
(10)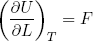 .
.
In words: the derivative of the free energy U with respect to the "deformation" L at constant temperature T is equal to the exerted force F.
For our rubber band we found that for small amounts of stretching, the force F changes linear with its length L,
(11)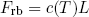 ,
,
where c(T) is a constant that depends on the temperature but not on L. If we integrate this expression with respect to L, keeping T constant, we find (according to equation 10)
(12)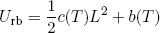 ,
,
where b(T) is the constant of integration. For fixed temperature this function describes a parabola that has a minimum for no deformation (at L = 0). It turns out that most materials in nature have a free energy of this form for small deviations from their equilibrium shape, i.e. almost any function looks like a parabola near a minimum (unless you design it very carefully).
Note that in the case of the suspended necklace we set U equal to the gravitational energy mgh integrated over the length of the necklace. In this context it is interesting to note that the Dutch physicist Erik Verlinde recently showed that the gravitational force law can also be "derived" from entropy arguments, like we did for the rubber band. But let's try not to stray off.
Free energy of a thin plate
Roughly speaking there are two modes of elastic deformation for a material: bending and uniform compression/stretching (see figure 3).
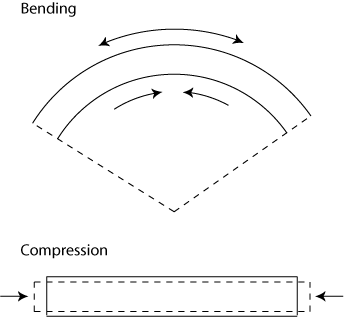
We will assume that in the buckled state of the tapeline, the biggest contribution to the total free energy comes from the flat U-turn, as this part seems to undergo the biggest deformation. Furthermore, we will assume that the flat part is in a mode of pure bending.
According to the textbook by Landau and Lifshitz on elasticity (or any other textbook on this topic) the free energy per unit length of a thin bended sheet can be written as
(13)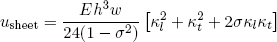 .
.
In this expression E and σ are respectively the 'Young modulus' and the 'Poisson ratio' of the material (see tabel 1). These properties can be directly measured and say something about the "(elastic) resistance to deformation" of a material. The dimensions of the sheet are incorporated by the parameters h (thickness) and w (width). Finally, κl and κt in this formula stand for the imposed curvatures (with respect to the initial shape) in the longitudinal and transverse direction. Note that the free energy is quadratic in the deformation, similar to what we found for the rubber band.
| Youngs modulus E | 210 GPa |
| Poisson ratio σ | 0.3 |
| Density ρ | 8000 kg/m3 |
| Width w | 16 mm |
| Thickness h | 0.1 mm |
The shape of minimum free energy
Figure 4 shows a schematic drawing of the of buckled tapeline.
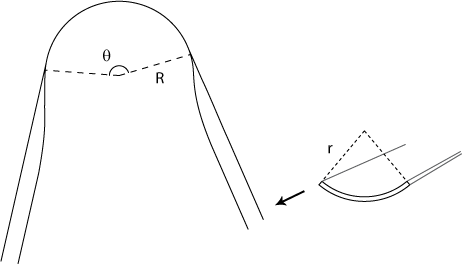
To find the total free energy of this shape we have to integrate equation 13 over the length of the flat part; with the appropriate local values for the curvatures κl and κt. One way to express the curvature at a point on a curve, is to draw a circle that approximately coincides with the curve near that point, and then taking 1 over the radius (thus large radius means small curvature).
In figure 4 we see that in the longitudinal direction (along the tape) the curvature of whole of the flat part is given by
(14)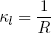 .
.
The curvature across this part of the tape seems to be zero (i.e. it's flat). However, in the free energy equation we are interested in the deviation from the natural shape, which has a radius of curvature r (see figure 4), so
(15)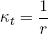 .
.
Because both curvatures in the flat bend turn out to be constant, integration of equation 13 boils down to a simple multiplication by the length, which is just R times Θ (if Θ is expressed in radians). Putting it all together, we find for the total free energy
(16)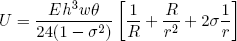 .
.
But we are not there yet. We still don't know what the radius R should be!
To find the equilibrium shape of the tapeline, we need to find the radius R for which the total free energy is a minimum. From calculus we know that we can find this minimum by setting the derivative of U with respect to R to zero,
(17)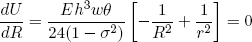 .
.
It is clear that this condition only holds if
(18)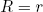 .
.
A remarkable result: the theory tells us that the radius of the flat buckled part should be exactly equal to the natural radius of curvature of the tape's cross section, independent of the material properties and the bending angle!
Let's put this "universal tapeline law" to the test.

And another one

Quite neat! Let's press on.
Critical moment
In the previous section we discovered that the buckled state of the tapeline can be accurately described by treating the flat part as a thin metal sheet that is bended. But what about the stiff, "rod-like" behavior before it snaps? Can we somehow predict the snapping moment?
The rod-like state before buckling
According to the same textbook on elasticity, the free energy (per unit length) of a bended rod is given by the surprisingly simple formula
(19)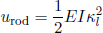 ,
,
where I is the 'area moment of inertia' of the cross section about the 'bending axis' through the center of mass of the rod, and κl is the imposed curvature of bending (along the tapeline). Mathematically,
(20)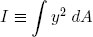 ,
,
where y is the distance to the bending axis of an infinitesimal part dA of the cross section. Figure 6 depicts the situation for our tapeline.
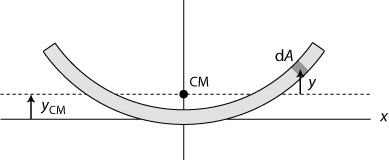
To simplify the calculations we can approximate the shallow circular shape of the cross section as a parabola,
(21)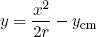 ,
,
so that by equation 20 the area moment of inertia becomes
(22)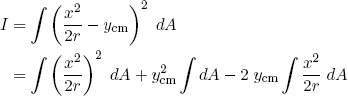 .
.
The center of mass ycm of the cross section is given by the formula
(23)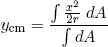 ,
,
which allows us to rewrite equation 22 as
(24)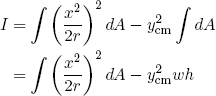 .
.
If we now approximate dA as
(25)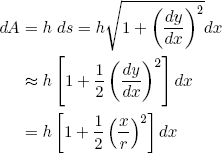 ,
,
and perform the integrations (from x = -w/2 to x = +w/2) we find
(26)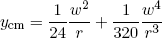
and
(27)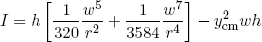 .
.
This is all we need to calculate the free energy of the rod-like tapeline as a function of longitudinal curvature (using equation 19).
The critical radius of curvature
To determine the critical radius of curvature at which the tapeline snaps, we can compare the free energy (per unit length) of the rod-like tapeline with that of the "sheet-like" or buckled tapeline discussed in the previous section. In figure 7 I plotted both free energies as a function of the longitudinal curvature κl. For a given curvature, the preferred state should be the one with the lowest free energy (orange line).
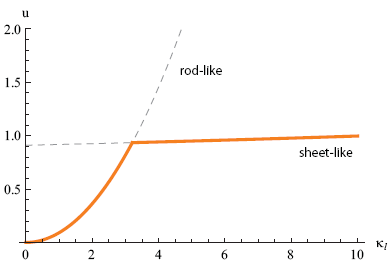
Our theory predicts that for small bending angles the rod-like state is preferred over the buckled state. But when the two lines cross, the flat shape becomes more favorable, SNAP!
If we take the derivative of the free energy with respect to the curvature, we find with how much force (or more precisely: with how much 'torque' or 'moment') the tapeline tries to oppose our bending (just like the derivative with respect to L gives us the force in the case of the rubber band). Figure 8 shows how the moment m in our basic model evolves as we increase the longitudinal curvature.
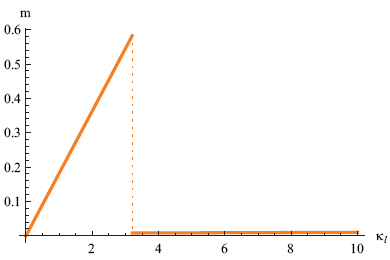
We see a sharp decrease in the resisting moment when the tapeline buckles. One can clearly feel this when one tries it with an actual tapeline.
From figures 7 and 8 we predict that the tapeline snaps when we bend it to a radius that is less than approximately 1/3 = 0.3 m or 30 cm. This is certainly in the right ball park, but in my experiments it buckles at a radius that is about twice as big.
A refinement of the simple model
Up till now we assumed that the tapeline behaves like an ideal rod for small deformations, and like an ideal thin metal sheet once it has buckled. In reality the tapeline goes through a more continuous transition from one state of deformation to the other. In 1954 Walter Wuest kindly worked out the full formula for the reaction moment of a bended piece of cylindrical shell [2]. His result is
(28)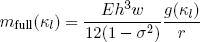 ,
,
where
(29)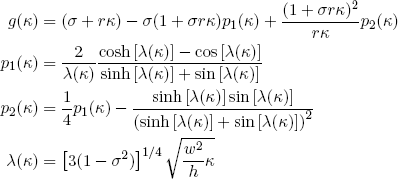 .
.
A monstrous formula, but let's put in the numbers anyhow. Figure 9 shows our basic model and the full theory of Wuest in a single graph.
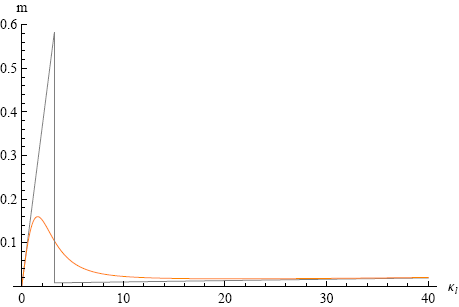
The two lines collapse for the limiting cases of low and high curvature, but the basic model clearly overestimates the critical curvature and corresponding bending moment. According to Wuest's formula the critical radius of curvature is about 1/1.6 = 0.63 m or 63 cm, which matches nicely with experiment.
We can also use the full theory to predict how far we can pull the tape out of its holder before it snaps under the influence of gravity. If we assume that the tapeline remains perfectly straight until it buckles (which is obviously not true), then the moment exerted by gravity would be
(30)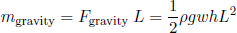 ,
,
where L is the extension of the tapeline. If no buckling is to occur, this moment must be smaller than the maximum in figure 9,
(31)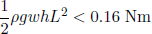 ,
,
or (putting in values from table 1)
(32)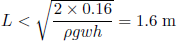 .
.
In reality the tapeline does not remain horizontal when it is extended, but bends down by about 30-40 degrees. If we correct for this in the moment exerted by gravity, we find a correction of approximately +0.2 m for the critical length. And it is indeed around 1.8 m that my tapeline buckles (if I pull it out carefully).
In the argument above we used the free energy per unit length to determine which state is thermodynamically favored for a given longitudinal curvature. This is justified as long as the whole tapeline is bended more or less uniformly.
However, once we go over the critical moment, it is not the whole tapeline that becomes flat, but only a small localized fold of radius R = r (as we saw in the first section). How can we incorporate this behavior into our model?
A two-phase model of the buckled state
We can think of any small piece of tapeline as being "surrounded" by the rest of the tapeline, so that according to our general entropy principle we must have
(33)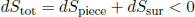 ,
,
for any small deviation from equilibrium. If we now assume that we impose a fixed longitudinal bending moment m on the tapeline, we can write
(34)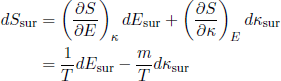 .
.
We have dEsur = -dEpiece (as before) and dκsur = -dκpiece, so that
(35)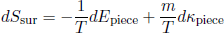
and
(36)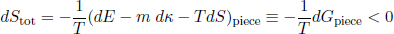 .
.
In this expression we defined a new function
(37)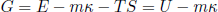 ,
,
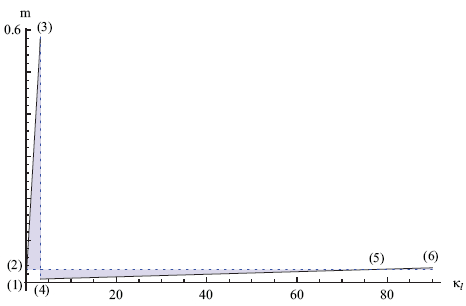
which is often called the Gibbs free energy (after the scientist Josiah Willard Gibbs). It is the Gibbs free energy (and not the free energy) that is minimized if the temperature T and moment m are held fixed. Since we know U and m as a function of κl (figures 7 and 8), we can (from equation 37) figure out the implicit relation between G and m. If we start from zero curvature κl = 0 and then let κl increase, we find the line G(κ) versus m(κ) shown in figure 10.
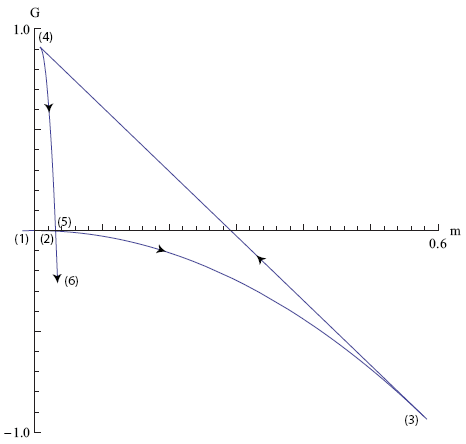
How should we interpreted this graph? Let's go through the numbers one by one. We start with a flat tapeline at point (1) and then slowly start to bend it. At point (2) the line crosses itself. This means that at a bigger curvature, there is another state of the tapeline with the same Gibbs free energy. As we go further one might expect that the tapeline would snap into the state that runs between (5) and (6), as this would lower the Gibbs free energy. But this is not what happens.
It is point (3) that corresponds to the critical moment of snapping that we calculated in the previous section (for the simple model). From point (2) to point (3) any piece of the tapeline is in what we call a 'meta-stable state'. In this state only a local perturbation or structural imperfection can make the tapeline buckle before we reach point (3).
Once a part of the tapeline buckles and becomes flat, this part will act as a 'nucleus' for the buckling of the neighboring parts. The nucleus will grow (more tapeline becomes flat) until any surplus stress in the tapeline is released. In the final state of equilibrium, the Gibbs free energy of the flat part must be equal to the Gibbs free energy of the surrounding (unbuckled) tapeline. Clearly, only the intersection point (2,5) in figure 10 can satisfy this condition.
The Maxwell construction
In 1875 James Clerk Maxwell introduced a convenient geometrical construction to find the intersection point directly from the m versus κ graph. The intersection assigns a single value to m, so in the m versus κ graph we are looking for a horizontal line. As shown in figure 11, such a horizontal line divides the m-κ relation in two areas (shaded). What Maxwell showed is that for the correct value of m, these two areas must be exactly equal. The left- and rightmost intersection points (2) and (5) then correspond to the two phases that are in equilibrium.
In case you were wondering why this construction works, let me shortly outline the argument. When we follow the path 2-3-4-5 in figure 10, we end up in the same point. Mathematically this can be stated as
(38)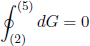 .
.
The little circle in the integral sign means that we go in a loop. The next step is to note that
(39)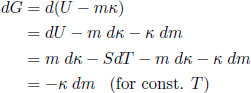 ,
,
where on the third line we substituted dU from equation 9 (with m dκ instead of F dL, because we are talking about a tapeline here). Plugging this into equation 38 finally gives
(40)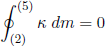 .
.
A condition which, after some thought, can be seen to correspond exactly to the Maxwell construction.
To summarize: in the buckled state the tapeline consists of two "phases" (let's call them 'plate-like' and 'sheet-like') that are in thermodynamical equilibrium at a constant value of bending moment m. Before the tapeline snaps, it is in a meta-stable state that can only survive if external perturbations or internal imperfections are not too big. When we surpass the critical moment, the extended tapeline will buckle no matter what.
Relation to the liquid-vapor phase transition
One can find many systems in nature that exhibit a phase transition that is similar to the one of our tapeline. A commonplace example is the phase transition of liquid to vapor.
Figure 12 shows the pressure versus volume curve of a piece of water. This curve is derived from a basic model (the so called 'Van der Waals model') of the free-energy versus volume relation of a parcel of water and gives a good qualitative picture of the actual behavior.
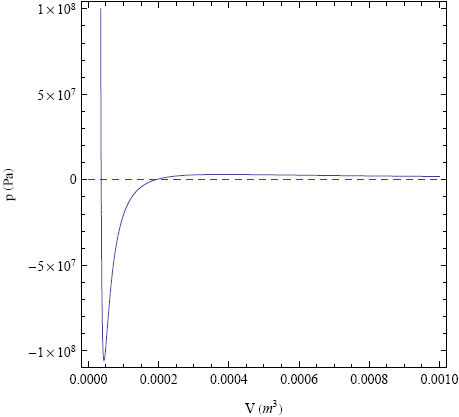
Essentially, the graph in figure 12 is an up side down version of the moment versus curvature graph of the tapeline, with a dense liquid phase on the left and a dilute vapor phase on the far right. The dashed line shows the equilibrium pressure derived from the Maxwell construction (about ~2x103 Pa at room temperature). At this pressure the water in your kettle could start to boil at 20 degrees Celsius. At 100 degrees Celsius this line shift up to 1 atm (~105 Pa), which explains why water can boil at this temperature at sea level.
Note that I said "can boil" in the last sentence. If we start with a piece of pure liquid water (i.e. without any initial bubbles that can act as nuclei), then the curve in figure 12 tells us that we must lower the pressure to about -1000 atm before the water "snaps" and starts to boil (note the minus sign, so we have to pull on the water). Between 1 atm and -1000 atm the water is in a meta-stable state, just like the tapeline before buckling. In this state only a big enough perturbation or imperfection (a gas bubble for example) can induce the liquid-vapor transition.
I would like to end this discussion with two striking examples in which the phase transition of water plays an important role (besides for cooking pasta).
The liquid-vapor transition in trees
Big trees have a big problem when it comes to pumping up the water all the way to their top leaves. A tree of, say, 20 meter high, needs to sustain a pressure of at least -1 atm near the top to overcome the hydrostatic pressure difference due to gravity.
The problem is not to pull with a pressure of -1 atm, this pressure can easily be achieved by letting the water evaporate from nanometer sized pores in the leaves (even in redwoods of more than 100m high, see figure 13), the problem is to keep the water in the tree's waterways from cavitating (boiling at low pressures). [4]

Trees have multiple strategies to protect themselves from cavitation. The two most important ones are (1) filtering of small particles and bubbles at the entrance (in the roots) and (2) division of its water channels into smaller units, so that in case of a cavitation event, it won't propagate through the whole tree. Finally a tree has some not yet completely clarified mechanisms to refill cells in which the water happened to cavitate despite the precautions.
Cavitation in beer bottles
Another dramatic example in which cavitation is key, is the famous party trick in which one blows out the bottom of a beer bottle (partly filled with water) by hitting it shortly but firmly on the top.
Some people manage to do this trick with their bare hands, but in our experiment we ended up using a Teflon hammer to get the desired effect (see figure 13).
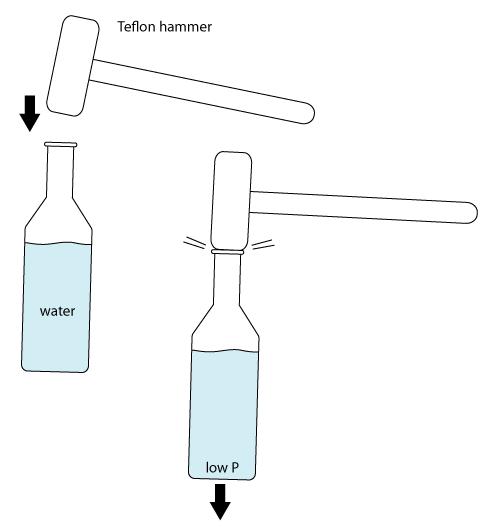
The idea is that the walls of the bottle accelerate downward faster than the gravitational acceleration of 9.8 m/s2, so that the column of water won't be able to follow. This makes that the bottom of the bottle will pull on the water, causing a negative pressure that can be big enough to make the water cavitate (i.e. boil locally). After the stroke, the pressure on the water will suddenly be increased to +1 atm again, resulting in a violent collapse of the cavities. During the collapse a narrow inward jet of water is focused toward the wall, which can exert enough force to make the glass crack.
The following movie shows a high speed recording of this party trick (a Friday afternoon project by me and a colleague).
References
- L. D. Landau, E. M. Lifshitz (1986), Theory of Elasticity, Vol. 7 (3rd ed.), Butterworth-Heinemann, ISBN 978-0-7506-2633-0
- W. Wuest, Einige Anvendungen der Theorie der Zylinderschale, Z. Angew. Math. Mech. 34, 444-454 (1954)
- K. A. Seffen and S. Pellegrino, Deployment dynamics of tape springs, Proc. R. Soc. Lond. A 455, 1003-1048 (1999)
- N. M. Holbrook and Maciej A. Zwieniecki, Transporting water to the tops of trees, Physics Today 61, 76-77 (2008)
