Your everyday world from a physicist's perspective
Huygen's cusp of coffee

When light from a distant source (like the sun or a light bulb on the sealing) hits a circular mirror (like the inside of a glazed coffee cup), the reflected light seems to be confined to the outside of a kind of kindney-shaped area (see figure 1).
As Christiaan Huygens showed in his Treatise on Light (1690) one can reproduce this shape by picturing the incident light as a collection of straight parallel rays that obey the reflection rule "angle of incidence = angle of reflection". In figure 2 I used the software package GeoGabra (which I can really recommend) to construct some of the rays.
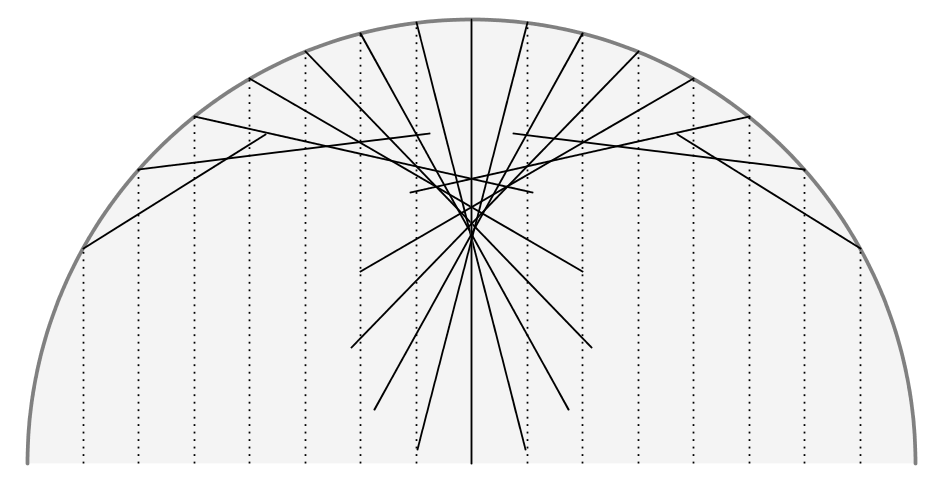
Following in the (rather big) footsteps of Huygens, I would now like to see if we can find an elegant formula or geometrical recipe that captures the shape of the 'envelope' without having to draw a lot of rays.
Shape of the cup caustic
To ensure that all rays stay within the envelope, we are looking for the curve that merely touches every reflected ray (i.e. the curve which is 'tangent' to the reflected rays). In figure 3 I drew two of the reflected rays, denoted by a(') and b('). The intersection point is highlighed by a big black dot.
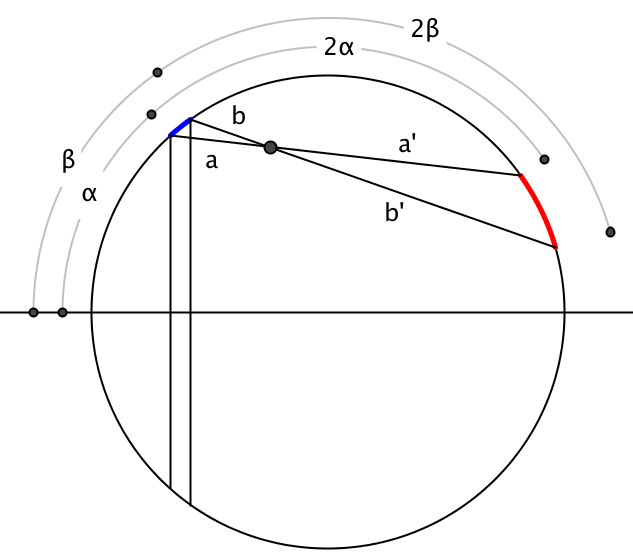
Our envelope curve should touch both rays and lay completely below them. This means that it will hit a and b', and not b or a' (as this would make the curve intersect a or b'). When we now let the incomming possition of the b-ray approach that of the a-ray, the touching point on b' should approach that on a (i.e. in the limit of overlapping rays, the point should be the same). Since the intersection point will always lay in between the two touching points, in the limit of b approaching a the intersection point must be at the touching point. In short: the challenge is to find the intersection point in the case of ray b approaching ray a.
The trick to find this intersection point consists of two steps:
- First one must recognise that when b approaches a, the length of b' will approach that of a', and the length of b that of a. This makes that, in the limit, we have two isosceles triangles with legs (a, b) and (a', b') which are 'similar' in shape (as they have the same angle at their tip, at the intersection point).
- Second, due to the reflection geometry (see figure 3) we have that the blue arc (β - α) is related to the red arc as (β - α) : 3β - 3α = (β - α) : 3*(β - α). In words, the length of the red arc is three times that of the blue arc.
Now, in the limit of a small arc, the length of the arc approaches that of the straight line connecting its end points. So in the limit of b approaching a, the blue and red arc become similar parts of our two similarly shaped triangles, with (red part) = 3*(blue part).
Conclusion: in the limit, the size of the isosceles triangle with legs (a', b') is three times that of the triangle with legs (a, b). This puts the intersection point, and thus the touching point, at 1/4 of the reflected ray. In figure 4 I traced this point as function of the position of the incident ray.

The pointy shape at the center of the curve is called a 'cusp' by mathematicians and the curve as a whole is called a 'nephroid'. Let's see if the theory is any good (figure 5).

It seems to be all right. And once you have written an article about caustics you start to see them everywhere...

Rollin' rollin' rollin'
Like a catenary curve is obtained by tracing out the locus of a parabola rolling over a line, it is a nice exercise in geometry to show that Huygen's cusp can be obtained by rolling a circle with a diameter 1/4th that of the outer circle over a circle twice its size (see figure 7).
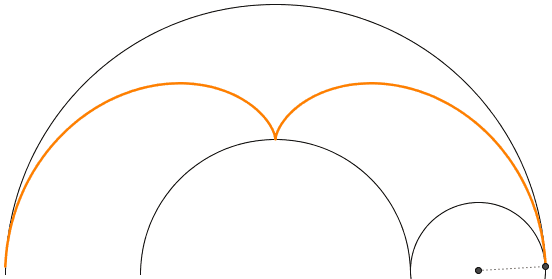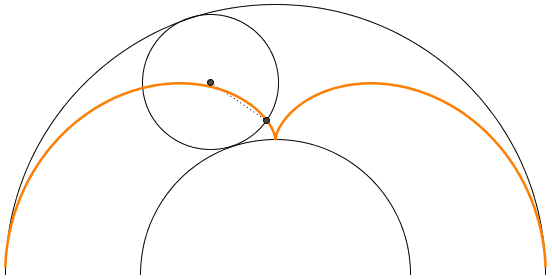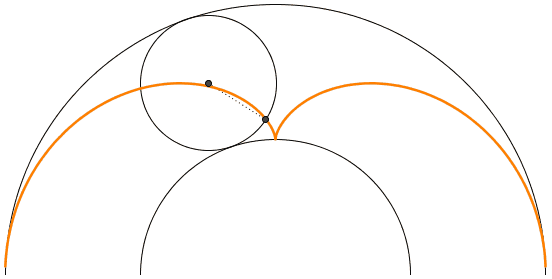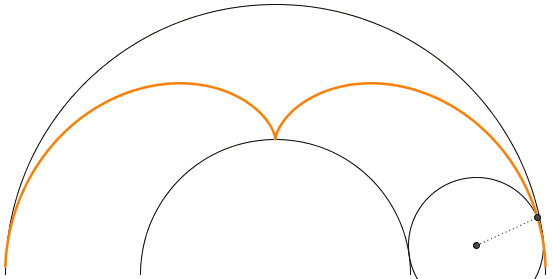
From this picture it is easy to derive a formula for the caustic curve in parametric form:
(1)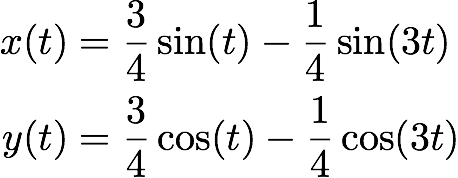 ,
,
where t runs from -π to π. If we now do a Taylor expansion of x(t) and y(t) around t = 0 (i.e. around the pointy part of the curve) and subtract 1/2 from y(t) (to put the point on the x-axis) we find for the first non-zero terms,
(2)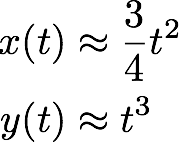 .
.
We can also write this as an implicit relation between x and y:
(3)![]() .
.
The form y2 ~ x3 is characteristic for the local shape of a 'simple' cusp and this is how they are usually identified by mathematicians.
Rainbow caustic
Another interesting case of reflection off a circular surface is examplified by the refraction and reflection of a bunch of parallel light rays inside a raindrop (see figure 8). The refraction on the droplet surface is given by Snell's law ni*sin(θi) = no*sin(θo) that we also touched upon in the article on specular reflection.
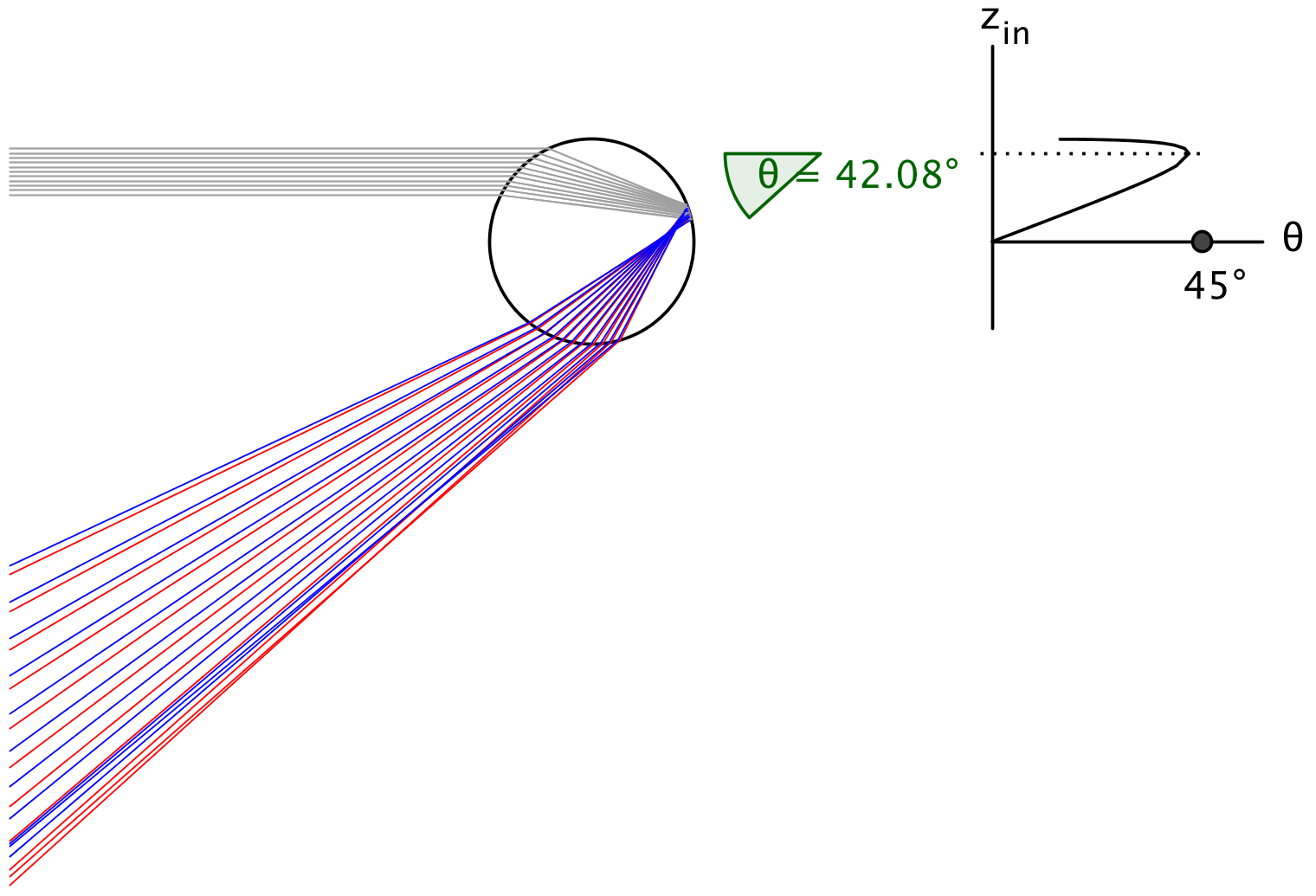
The small graph in the top right corner of figure 8 shows the final emerging angle θ of the reflected ray as a function of the vertical position of the incident ray. It shows a maximum angle of about 42 degrees. From this we can deduce two important things:
- No light emerges at an angle greater than 42 degrees from the incident light direction.
- Near the maximum the light rays have a higher density (i.e. greater intensity) than far away from the maximum (because of the slower variation here).
To make the connection with the Huygen cusp discussed above, we could also say that the reflected light is contained in a finite 'envelope' (a maximum angle) sealed by a bright 'caustic' curve.
As discussed in the article on specular reflection, the refractive index of a medium depends on the frequency of the light. So red light has a slightly different refractive index than blue light. This means that the maximum angle for red light is slightly different (bigger in this case) than for blue light, as indicated by the red and blue rays in figure 8.
So if we look at the light emerging from a big collection of raindroplets which are illuminated by the sun (assumed to be straight behind us), we see no light emerging from an angle bigger than 42 degrees up in the sky, but then, if we look lower, we first see a bright red band, then a bright green band and finally a bright blue band (and every color in between). After these "bands" we see a slight white glow. This is where all the colors are mixed in equal amounts. In other words: we see a rainbow!

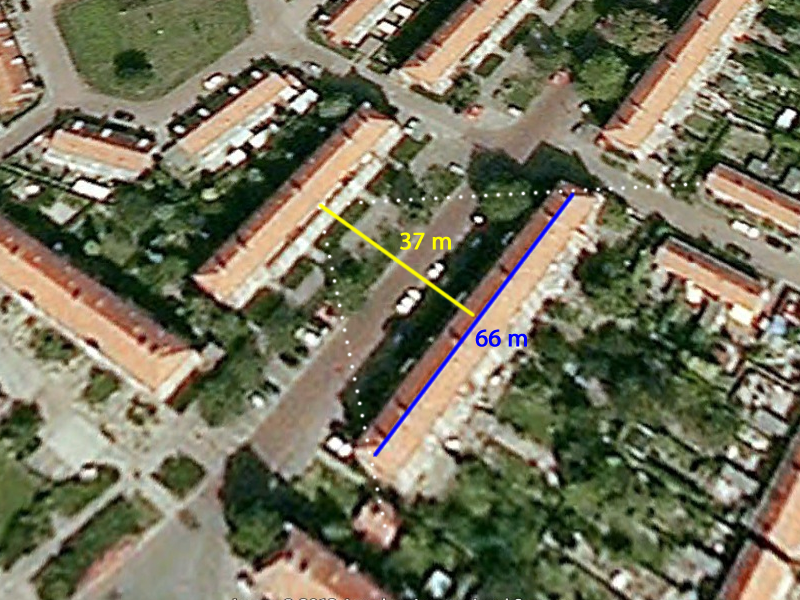
To check if the bow really spans the angle of 42 degrees we get from the theory, I looked up the building in figure 9 on Google Maps and measured the distance from where I took the picture (see figure 10). Indeed we find a viewing angle of about tan-1(33m/37m) = 42 degrees.
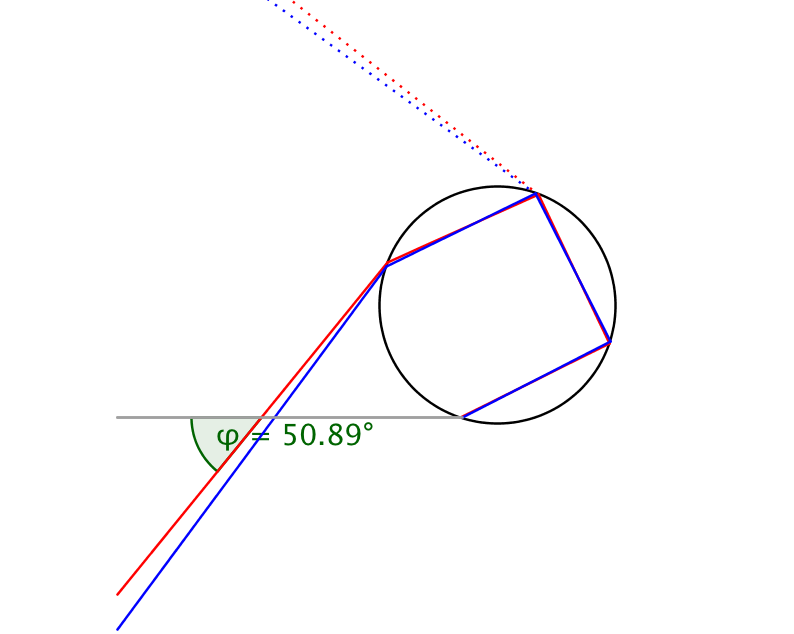
If you look carefully at figure 9 you can actually see two rainbows. A second, fainter bow appears at an angle of about 51 degrees. It has its colors reversed and it has a slight white glow on the outside of the bow.
This secondary bow is explained by a double reflection within the droplet (see figure 11). This time the incident light causing the bow enters the droplet at the bottom half, resulting in a reversal of the colors. With every reflection inside the droplet some light is also transmitted, which explains why two reflections give a fainter bow than one reflection.
The dark band in between the primary and the secondary bow is called the 'band of Alexander', named after Alexander of Aphrodisias who already noticed it in 200 AD.
