Your everyday world from a physicist's perspective
Specular colors
Some days ago my blue ballpoint pen was leaking ink like a battered bucket. A big pool of ink was forming on my desk, and then I noticed something remarkable: my fluorescent desk lamp looks red (!) in its reflection from the puddle of blue ink.
Excited about my "discovery", I quickly ran to the bookshop to get some more pencils: they have red, blue and green.

This is what I found. The pool of red ink reflects a greenish light, the blue ink reflects red and the reflection from the green ink seems to be shifted to the blue (with some imagination).
How can we possibly make sense of this? Shouldn't ink from a blue pencil reflect blue light? Nature must be playing tricks on us.
The colors in my desk lamp
Before we look into the properties of the ink, let us first find out what kind of light the desk lamp is producing. A neat way to do this is by looking at its reflection in a compact disk (CD).

A CD does not solely reflect according to the usual mirror-rule 'angle of incidence equals angle of reflection', but it also reflects at some other peculiar angles. This is a true miracle in its own right and has its origin in the spiraling pattern of grooves on the surface (hint: interference).
Let's not stray off. The main point is that the angles are different for different colors of light. And it is a lucky coincidence that the spacing between the grooves is just right for the range of colors we are interested in (i.e. the colors that our eye can see). So from the picture above it is clear that our fluorescent lamp emits four distinct colors: blue, green, yellow and red.
But wait a second! If one looks carefully at the colored reflection spirals one will notice that the blue reflection shows both of the discharge tubes of the lamp, while the green, yellow and red reflection only show one tube. As it happens, the lower tube of the green reflection overlaps with the upper tube of the red reflection. This mixture of red and green light is interpreted by the eye as yellow (one can check that there is no yellow in there by letting the light first pass through a small hole in a piece of paper).
So our fluorescent desk light emits three distinct colors: red, green and blue. Note that this is very different from light from for example the sun, a glowing light bulb or a candle. These sources emit a (nearly) continuous spectrum of colors (i.e. red, green and blue and all the colors in between). Red LEDs on the other hand only emit red light (try it!).
This shows that it is very important to know something about the light source in trying to solve mysteries involving colors. Most materials can only reflect the colors that are already in there! However, this little light source investigation doesn't quite solve our initial ink conundrum.
Reflection from smooth surfaces (i.e. mirrors)
If you ever looked from the side at a straw in a glass of lemonade, you can probably already guess what a wonderful thing I will tell you now: the straw appears to be cut in two by the liquid to air interface!

From experiment it is known that almost all effects concerning the bending of light (when it passes from one medium into another) can be neatly described by one very simple formula (first written down in 984 and later (1621) rediscovered by the Dutch astronomer Willebrord Snellius),
(1)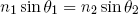 .
.
In this formula n1 and n2 are two numbers, called 'indexes of refraction', that describe the propagation of light (of a certain color) through the two media. For visible light, n is about 1.0 in air, 1.5 in most glass types and 1.3 in water, although it will slightly vary from red to blue (which partly explains how rainbows are formed). θ1 and θ2 are the angles the "rays of light" make with the surface normal in the specified medium (see figure 4). Together with the mirror rule mentioned above, you probably learned this very useful rule by heart at school (at some point).
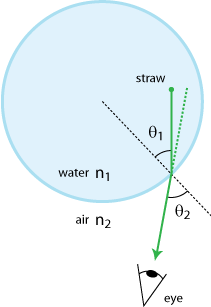
If I was writing a textbook on physics I would now show you how the mirror-rule and the law of Snellius are correctly "predicted" by the different theories we have for light. But as this is not a textbook, let's skip over the "boring stuff" and instead have a look at two formulas (called the 'Fresnel equations') that complement Snell's law and the mirror-rule by telling us how much light (i.e. what percentage) will be reflected at different kinds of interfaces:
(2)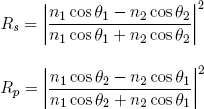 .
.
There are two expressions for the reflection probability, one labeled 'senkrecht' (which is German for perpendicular) and one labeled 'parallel'. This is because a beam of light of a certain frequency (or photons, or electromagnetic waves, or however one wants to call it) can always be decomposed in two types, two 'polarizations'. Equation 2 tells us that light polarized perpendicular to the plane of incidence has a different chance to reflect than light polarized parallel to this plane (for certain angles). Polaroid sunglasses are designed to block the type that reflects most strongly (see figure 5).

For normal incidence (θ = 0) there is no way to discern the two polarizations and the two formulas give the same answer:
(3)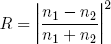 .
.
The Fresnel equations (eqs. 2 and 3) give the general law for the amount of reflection from smooth surfaces. But to see what this law implies for our pool of ink we still need some kind of expression for n.
The refractive index of ink
Finding the refractive index of a material is a very challenging problem in quantum electrodynamics. Only for some simple substances it can be done by direct calculation.
Luckily one can write down a fairly general equation for the form of the refractive index for many common materials (which is known to work from experiment and electrodynamics calculations). For not too dense materials like air (and probably also our ink particles) we will have something like
(4)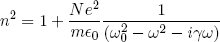 .
.
In this equation N is the density of atoms (or ink molecules), e and m are the (effective) charge and mass of electrons in the material and ε0 is a constant of nature (called the 'dielectric constant of vacuum') that has to do with the coupling between light and matter.
The most interesting part of equation 4 is where the dependency on the (angular) frequency of the light, ω, comes in. It is clear that n2 will become very large if ω approaches the value of ω0. The parameter ω0 is what could be called the 'resonance frequency' of the material and has to do with the driving of the electrons in the material by the beam of light (like parents can excite their children by "driving" (i.e. pushing) them with exactly the right timing on a playground swing). Note however that most materials (if not all) are a bit more complicated than a simple "swing" and will have multiple optimal driving frequencies. We could incorporate this in equation 4 by writing the last term as a sum over similar terms with different ω0s (and different weight factors). But let's not complicate things more than necessary (as it will not add any significant new features). Finally, γ represents a friction (or energy dissipation) that works against the motion of the electrons and is responsible for the heating of the material when light passes through.
For dense materials (like glass and water) one needs a correction on the left hand side of equation 4 to account for the interaction between neighboring charges in the material:
(5)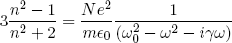 .
.
The optical properties of metals - and other substances in which (some of) the electrons can move more or less freely - can be described by a formula like equation 4, but with the resonance frequency set to zero (since there is no "restoring force"):
(6)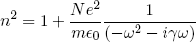 .
.
For a metal γ is directly related to the electrical resistance experienced when trying to pass an electrical current through.
As one might have noticed on closer inspection of equations 4 through 6: the right hand side is negative for some values of ω, whilst on the right hand side we have n squared. This means that in general n will be a complex number (I bet not everyone has learned this at school!).
The figure below (figure 6) shows a graph of the real part Re[n] and the imaginary part Im[n] of n for our model ink (equation 4). I've set the resonance frequency ω0 to 2.7 petahertz (2.7 x 1015 oscillations per second) which corresponds to the frequency of red light. One can see a clear peak in the imaginary part around the resonance frequency, which brings us to the next subject of this exposition.
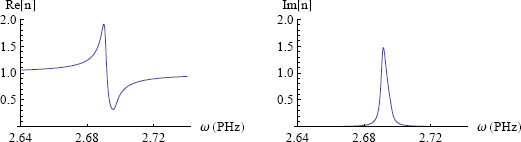
Absorption
It turns out that the complex part of the index of refraction corresponds to an attenuation (gradual decrease) of the light intensity I as the light gets deeper into the material,
(7)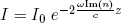 ,
,
where I0 is the intensity at the surface (which I'll take to be 1 in what follows), c is the speed of light and z is the distance from the surface. This attenuation has two causes:
- light that is eventually reflected out from the surface and
- irreversible absorption processes inside the material (light is transformed to heat).
From Fresnel's laws we already know how much of the light will be reflected. Now, to find out from this how strongly the material absorbs light of a certain color we can use that
(8)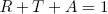 .
.
Or in words: the chance that the light is reflected R plus the chance that it gets all the way through T plus the change that it is absorbed A, should sum to one (i.e. 100%, something has to happen!).
If we make the slab of material very thick (say, infinitely thick) and there is some absorption, then no light will get through in the end, so we can set T = 0,
(9)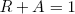 .
.
Now suppose that, in our thick slab of material, there is a chance σ per unit length that the light will be absorbed, then we have
(10)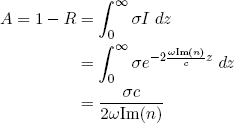 ,
,
or
(11)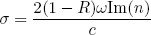 .
.
In figure 7 I've plotted the reflection chance from Fresnel's law (equation 3) and the absorption chance per unit length (equation 4) for our model ink (figure 6).
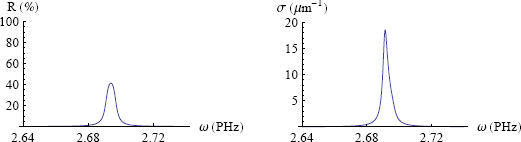
Lo and behold. The light frequency at which the ink absorbs best, coincides with the frequency of maximum reflection. This is why blue ink reflects red!
We have found a very general phenomenon: if one makes a smooth surface (i.e. a mirror) out of a material that absorbs some color very strongly, then that color will also be reflected most strongly. Miraculous, but true. The mobile electrons in metals make that they absorb all colors approximately equally, and that's why the mirror in your bathroom consists of a thin, smooth layer of metal (usually silver).
One might think that I'm a bit silly, because if blue ink mainly reflects red light, as I am telling you, then why does it usually look blue (and therefore is called 'blue ink')? Well, in many circumstances light is not reflected toward the eye directly upon first encounter with the material. Instead it bounces around a bit between the colored fibers of the paper and one will only see diffuse light emerging. Now suppose that at each bounce 20% of the red is reflected and the rest is absorbed, then after three bounces only (0.2)3 = 0.8% of the red has survived and will be overwhelmed by the other colors that are not so strongly absorbed. In other words at some level of diffusive scattering, the enhanced absorption will dominate over the enhanced reflection of the red.
Many, many other mysteries involving light interacting with matter can be understood using just these equations, and that's the beauty of it. I wish you a colorful and happy new year!
References
- Richard P. Feynman, Robert B. Leighton and Matthew Sands, The Feynman Lectures on Physics, Vol. II, Addison-Wesley (2006), ISBN 0-8053-9047-2
